NumberOfDiscIntersections

Compute the number of intersections(相交) in a sequence of discs(圓盤).

We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses(半徑) of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

A[0] = 1 A[1] = 5 A[2] = 2 A[3] = 1 A[4] = 4 A[5] = 0

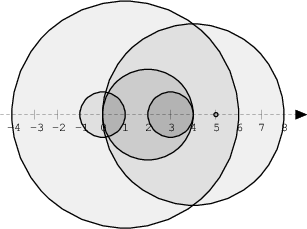
There are eleven (unordered) pairs of discs that intersect, namely:

• discs 1 and 4 intersect, and both intersect with all the other discs;
• disc 2 also intersects with discs 0 and 3. Write a function:

func Solution(A []int) int

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Given array A shown above, the function should return 11, as explained above.

Write an efficient algorithm for the following assumptions:

N is an integer within the range [0..100,000]; each element of array A is an integer within the range [0..2,147,483,647]. Copyright 2009–2021 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.

題目大意

A[0] = 1, 代表在(0,0)的位置上有一個半徑為1的圓. 找出圓相交的個數

解題思路

• 方法一: 對於第i，j個圓來說，如果兩個原要相交的話

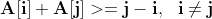
參考SolutionDirect. 時間複雜度為O(n^2)

• 方法二 也就是將原來的二維的線段列表變為2個一維的列表 首先遍歷數組A得到A[i]+i組成的數組i_limit，以及j-A[j]組成的數組j_limit。然後再遍歷數組i_limit中的元素S，利用二分查找算法得到數組j_limit中不大於S的元素個數。前一個操作時間複雜度是O(N)，二分查找算法時間複雜度是O(LogN)，因此最終的時間複雜度為O(N*logN)。參考Solution。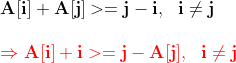

來源

• https://app.codility.com/programmers/lessons/6-sorting/number_of_disc_intersections/
• https://github.com/Anfany/Codility-Lessons-By-Python3/blob/master/L6_Sorting/6.4%20NumberOfDiscIntersections.md
• https://rafal.io/posts/codility-intersecting-discs.html
• https://github.com/tmpapageorgiou/algorithm/blob/master/number_disc_intersections.py

解答

https://github.com/kimi0230/LeetcodeGolang/blob/master/Codility/Lesson/0006.Sorting/NumberOfDiscIntersections/NumberOfDiscIntersections.go

package NumberOfDiscIntersections

import "sort"

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

// 時間複雜 O(n^2)
func SolutionDirect(A []int) int {
    count := 0
    for indexI, valueI := range A {
        tmpArr := A[indexI+1:]
        for indexJ, valueJ := range tmpArr {
            if valueI+valueJ >= indexJ+indexI+1-indexI {
                count++
            }
        }
    }

    return count
}

// 時間複雜 O(nlogn) or O(n)
// TODO: 待研究
func Solution(A []int) int {
    iLimit := make([]int, len(A)) // 左
    jLimit := make([]int, len(A)) // 右
    result := 0

    for i := 0; i < len(A); i += 1 {
        iLimit[i] = i - A[i]
        jLimit[i] = i + A[i]
    }
    // 針對iLimit中的每個元素，利用二分查找算法，找到其不小於jLimit中元素的個數
    sort.Ints(iLimit)
    sort.Ints(jLimit)
    for idx, _ := range iLimit {
        end := jLimit[idx]

        // Binary search for index of element of the rightmost value less than to the interval-end
        count := sort.Search(len(iLimit), func(i int) bool {
            return iLimit[i] > end
        })

        // 因為i=j時，A[i]+i 肯定不小於j-A[j],也就是說多算了一個，因此要減去1。
        // 減去idx是因為圓盤A和圓盤B相交，次數加上1了，圓盤B和圓盤A相交就不用再加1了。
        count = count - idx - 1
        result += count

        if result > 10000000 {
            return -1
        }

    }

    return result
}